Snell's Law: Part The First

{Part  II −−>}

When light crosses from one medium to another of a different density, its speed and wavelength change.  Where it strikes the new surface at an angle, the transmitted wave is refracted, that is, the light changes direction.

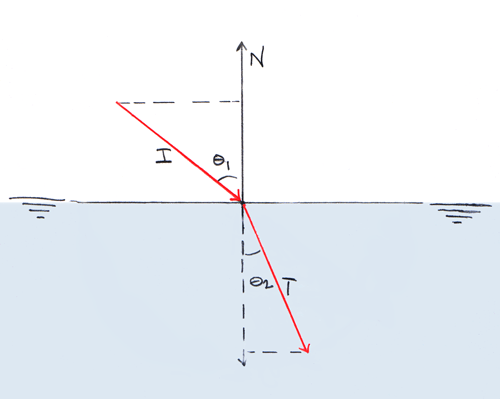
Light which intersects a surface is incident.  The light which passes through the surface is transmitted.  The line perpendicular to a surface at a point p is normal to the surface at that point.   According to Snell's Law, we can assign to each medium a constant value η (eta), called its index of refraction (IOR), which satisfies the following relationship:
(1)                                                   η₁ sin θ₁ = η₂ sin θ₂ 
where η₁ and  η₂ are the indices of refreaction of the first and second media, respectively, θ₁ is the angle between the incident ray and the surface normal, and θ₂ is the angle between the transmitted ray and the normal.

Fig. 1

In Fig. 1, incident ray I strikes a new medium, and the transmitted ray T is refracted.  Each is shown as the hypotenuse of a triangle.  If both I  and T are drawn with a length of 1 (if they lie on a unit circle), then the opposite sides of the triangles will have lengths sin θ₁ and sin θ₂   (mouse over the image).  According to Snell's law, the relationship between these two lengths and their corresponding angles is completely determined by the constant ratio η₁/ η₂:

 

I will explore this equation in depth over several blog entries.

Assumptions

{  Edit: this section has been reworked.  I seek clarity in method and presentation.  If a question appeared here and vanished, I will visit it at a later point.  If you think I should retain, and strike, prior text  ( like so ) let me know.   Thanks to Peter Schaefer for assistance with assumption ii. }

i) The surface normal is vertical in the reference plane.
ii) The transmitted light will lie in the same plane as the incident ray and the surface normal.  In the diagram, there is a single transmitted ray.

The first assumption is made for simplicity.  For rigid geometric objects, relationships between angles are invariant under translation and rotation.  For example, if you print out Fig.1 and set it in front of you on the table, spinning the page around will not change the measure of any of the angles.  This problem is easier to solve for N = (0, 1) than for arbitrary N.

I assume (ii) as part of the definition of Snell's Law.  That is, it is a physical result. 
The difficulty is this.  As mentioned in the nVidia paper, equation (1) alone does not appear to restrict T to the same plane as  I  and N.  For, what is to prevent you from cheerily rotating T around the dotted line and forming a cone?  Nothing.  The interior angle remains θ₂ all the way 'round. Thus, by the Who's Going to Stop Me Theorem T need not lie in the given plane.  This may be done independently of a cheerful disposition.
However, I have given the incident ray and surface normal as vectors.  Together, I and N give the plane in which T will lie.  That is the point of the diagram.  I will state the restriction mathematically and account for it later, when I move the result to 3 dimensional space.

Onward.


For computation on graphics hadware, it is desirable to express Snell's Law in vector notation.   Thus,

Call the incident vector  I, the normal to surface N, and the transmission vector T. Assume I, T and N are normalized (each has a length of 1), and all lie in the same plane.  Then,
GIVEN: η₁, η₂, the indicies of refraction of the two media,
LET:
(2)  N = (0, 1)
      I = (–sinθ₁, cosθ₁)
     T = (sinθ₂, –cosθ₂)

The dot product of two normalized vectors gives the cosine of the angle between them.  Hence,
(3)   I•N = cosθ₁

I will also need the following trigonometric identity:

The Problem: Give T as a vector equation in η₁, η₂, N, and I.

This requires two steps , which may be done in any order.

I. Calculate T for any given η₁, η₂, N and I.

If I rewrite sinθ₁,  sinθ₂  and  cosθ₂  in terms of  cosθ₁ = I • N,  I can give each component of T as a vector equation.

sinθ₁ :  By (3) and (4), sinθ₁ becomes

sinθ₂ :  By Snell's Law (1),  sinθ₂ = (η₁ /η₂)sinθ₁   and by (4),

cosθ₂ :  Substituting this value of sinθ₂  into (4):


We can now give T = (sinθ₂, -cosθ₂):

This is correct, but in the vector T = (t₁, t₂), t₁ and t₂ have been solved separately.  I seek slightly more than this; I want to solve both simultaneously.  Hence,

II. Give T as the sum of two vectors.

Specifically, I want to write T as a linear combination of the two given vectors, N and I:

(9)        T      =     αI     +    βN ,         α, β constant:

       

This is another way of writing a pair of equations, with unknowns α and β:

(10)       sinθ₂ = –α sinθ₁

           –cosθ₂ =  α cosθ₁ +  β

α: The first equation gives α directly.   α =  –(sinθ₂/sinθ₁)   which, by (1), is

(11)       α = –η₁/η₂

β: Substituting this value of α into the second equation,

(12)       β = (η₁/ η₂)cosθ₁ − cosθ₂

Now the two steps can be merged.  Using the values for cosθ₁ and cosθ₂ in (3) and (7),

Substituting the values for α and β in (11) and (13) into T = αI + βN  gives  the desired relation:

                   

I have not derived a new formula, nor have I developed one of my own.  The above equation is an exact restatement of Snell's Law, in vector notation.

{Thanks to CodeCogs for their free LaTeX equation editor and image generation.}

{Part  II −−>} 

Numerical Methods

Sometimes, while I am working, I will run across sentences like this:
...which can be computed according to the following formula given by SoAndSo, SomeDate:  {SomeFormula}.

I will stop reading, close the paper, and work out the relationship for myself.

There are several reasons.

The first is about me.  I doubt solutions until I can demonstrate them to myself.  I do not value memorization at the expense of comprehension.
We may rearrange a problem however we wish using the rules of algebra and geometry.  If mathematics is a language, it has only a few words.  The rest is concision and clarity.  I think the student who can manipulate 12th century Persian Algebra and weild a protractor, compass and straightedge, and know what she is up to, may gain ground as quickly as she like on University coursework in computer science and programming.

I seek to describe and solve problems in acoustics, wave propagation, and signal processing.  The state of sound design tools is poor, and their advancement is hindered by errors of logic and observation, accepted as common knowledge and understanding.  To identify, describe, and solve these problems, it is sufficient to construct mathematical descriptions of sound, and account for the physical properties in a consistent way.  The errors are basic.  They can be demonstrated with a walk down the street; walking around a streetlight; listening to a train.  To make the properties of waves more intuitive and accessible --and to insure that they are correctly accounted for-- I have constructed a series of analogies to light: construction of an image, its properties, and the mechanics of wave propagation.  My solutions will follow directly from known mathematical results, and observation of the physical world.  I work out each problem from scratch. I teach myself the necessary math, mostly out of old Dover press paperbacks.

Patents and Mathematics
The second reason is about mathematics.  All mathematical results follow inescapably from the definitions and rules of manipulation.  (Which is not to say easy.)  A valid result is one which can [and will] be obtained independently by anyone [and everyone].  The proof is demonstration.  The bracketed words are the heart of the matter.

Not everyone is clear about this.  That is a problem, and each person has to decide how to handle it.   I choose not to be slowed down.  I do not have time to pretend that a person can own math.  I sequester myself; I will not copy another person's mind. I have always worked this way, and I love it.  The history of mathematics is free to use, and any results I derive from it are equally free.  So therein I will work.

I am not overly fond of Modern Abstract Mathematics.  Proponents often confuse themselves with the tools they advocate, and say what anyone can understand  in a way that only a few people can.  The proofs usually run backward, never identifying the structure of the problem.  So I practice going backward in time, to obtain the answer.  Each time I go back, what I find is worth the trip.

There is more at stake than money, time, or the enjoyment of mathematics.  Math belongs to no one.  We are ethically responsible to make it accessible.  We also have a rational responsibility.  Mathematics is a logically elaborated structure; within it appeal to authority is baseless.  Any declaration of ownership can be shown to be invalid.
The last two sentences are exact.  There is no other ground to take.

It's alright.  I won't use or examine methods which claim to ownership.  If you Own algorithms, I won't read your paper; it can sit quiet on the shelf. I do not want to know anything about what you are up to.  If we stumble into each other, there will be no question.   All I will need is a chalkboard.

Onward.

Example, With Train

 Recently, I was reading a paper on efficient computation of caustics.  Here is where I stopped:

"Let's forget about reflection for a moment and see how transmitted photons are refracted according to Snell's Law, which states that:  η₁ sin θ₁ = η₂ sin θ₂,   otherwise written as:
IOR = η₁/η ₂ = sin θ₂/sinθ₁
In the preceding equations, η₁ and η₂ are the indices of refraction for the respective materials, and θ₁ and θ₂ are the incident and refraction angles, as shown in Figure 2-2. The index of refraction, IOR, can then simply be written as the ratio of the sines of the angles of the incident and refracted rays.
Snell's Law is not easy to code with this formulation, because it only imposes one restriction, making the computation of the refracted ray nontrivial. Assuming that the incident, transmitted, and surface normal rays are co-planar, a variety of coder-friendly formulas can be used, such as the one in Foley et al. 1996: [....]"

[from, http://http.developer.nvidia.com/GPUGems/gpugems_ch02.html . Italics mine.  Diagram omited.]

I have left out the next line.  I glanced at it, but it was unfamiliar so I stopped, closed the paper, and began working from scratch.  The citation was just the icing.

   This is from a book called GPUGems which is available for free on nVidia's website. This is a great idea, and I hope more companies catch on.  I work alone on a limited budget and the GPUGems series, and nVidia in general, distinguish themselves for free numerical methods, heaped with examples and explanations.  When I am employed, one of my first treats to myself will be to purchase the whole series.
It makes me think selling numerical methods is easy, as long as you don't patent them.  You print them, and then you can sell them.  People will buy them so they can use them.  There's a word for this kind of cooperative-competitive market model, but I just can't remember what it is....


In this case, I do not think there is a problem.  Citation is essential to research and the propagation of knowledge.  I can investigate further if I want, and the author is a good professional  neighbor to boot.  But why don't we solve the problem anyway?  How do people resist?

Problem:  Assuming that the incident, transmitted, and surface normal rays are co-planar, derive a [varitey of] coder-friendly formula[s] for the direction of the transmitted ray.

___________

Update:  I am deeply indebted to Professor Herbert Gross for his clear and concise language.

  Inescapable at last supplies what is wanting in the troublesome expression, self-evident.

Professor Gross' video lectures at MIT's Open Course Ware can be found here.

What I am up to

    If you are my friend, you may wonder what I have been doing for the last year and a half.   I constructed an experiment in me: a way forward with my life.  I built a story.  In this story I can be whatever I wish; I can do anything, and reach to the top of whatever I choose, unassisted.  This story also gathers my body and heart and brings me closer to those I love.

     I have chosen to work in sound design and have been teaching myself everything I need.  Here is an approximate list (Entries in braces, I have not yet begun):

Music:
Mixing
Mastering
Learn new instruments
Instrumentation
Song styles
Counterpoint

Recording:
Field recording
Studio projects

Mathematics:
Advanced Calculus
Differential Equations
Linear Algebra
Signal Systems and Transforms
(Harmonic Analysis)
Algorithms and Numerical Methods

Visual asset design:
Planning and lighting a scene;
Hard surface 3D modeling;
Organic modeling;
Rigging and Animation
Asset creation:
    Texture and material construction;
    Unwraps, Normal maps, <*.maps>
    Optimizing and Exporting game-ready content

Code:
C++
Game Engine:  UDK
    Familiarize myself with all features of the interface
(DirectX)
(XAudio2)

Writing:
The mechanics of language and the elements of storytelling.

Game project:
Construct a game world
     Build all assets from scratch: visual, audio, code.


Selection Criteria:
Some topics may appear unusual.  What do normal maps have to do with sound?  Why hard-surface modeling and animation before XAudio2? There are several reasons:

     Sound is motion:  Sound does not exist without movement.  Game worlds are nonlinear, interactive.  At least two questions arise: What moves? How?  New tools must provide reusable, generalizable answers to these questions.   But to have motion, there must first be a world.

     Logical integration: A game editor like UDK is a complete logical environment.  Everything in the world - a 3D mesh, the sound of a foostep, a light - is an object. In game design, a good tool is a piece of object-based logic: a set of rules by which objects can be made to work together.  Making tools means developing a code base.   And in relation to other game objects, sound is a result:  New audio tools must be integrated into the existing logic which operates and animates in-game objects.

     Spatialization:  Real-time phase manipulation in 3-space is a defining question of the video game.  Representing audio in 3D is an open question. Epic Games (UDK), for example, takes the position that it is hard, so do not try, i.e. record in mono and pan it. This is the least effective way to spatialize.  A sound image is a field: movement changes the phase relationships within the field, and from these phase relations, we distinguish position.  Panning a mono file does not reproduce, or simulate, motion in a field.

Fortunately, graphics programmers and hardware developers have constructed a considerable body of knowledge and experience in the attempt to simulate a similar question of light propagation. Efficient computational methods in harmonic spaces exist, they have physical representations, sample code is available, and specialized hardware for its execution lies in every game console. I believe apprehending and adapting these graphical and geometric methods is the best and fastest way forward; the mathematics and programming skills are fundamental to the question of audio in a game world.

     I love it: If it is on this list, I do no tire of it. I wake in the middle of the night to do it. I dream about it. I draw crowns in my Advanced Calculus book, and stay up until 4AM recording for a friend.


The Job I Seek:
I want to do the everyday work in audio design. I want to record and make sound effects; match audio to keyframe animations; record, edit, mix and master dialogue. Compose and arrange. This is what I do with all of my time, when I am free. I am at my best when I am the least experienced person in the room. I learn quickly, and I love it.

I do not want to be a team lead or a programmer. Making new tools, for me, is an outgrowth of hands-on work with audio. I have begun building what I need to do that job better and faster. I believe many things can be done which are not commonly believed possible, but I do not have a paradigm to peddle: I am always willing to be convinced. That is why I state my position clearly, and defend it. Code is invention and construction: to posit new ideas and test them requires believing they can be done, and trying every way to make them work.

I have a rough map in my mind of the game engine, and every way audio occurs. I also dig further into the methods that exist, to clarify the map. For each place there is sound, I have thought through at least one way to move forward. These structures are primitive, but similar, and often identical, to what the best audio software companies are building. I do not do this by examining their products. I figure it out first, alone, then I check to see who else knows. This is how I find Valve and iZotope. It is better than finding them. I know how to begin building these tools myself, because those elements I understand, I, too, have invented.

I do not expect you to believe me on my word. I expect to convince you. I will post a series of blogs on various audio and game topics, with examples of my own work.

The rest of me:
There is a parallel story which accompanies these mechanical steps: a boy and a wolf, bound together, ducking in and out of the lands of snow. The mechanics of belief are important; they demystify momentum, and demonstrate that anyone may do likewise. Watever we make up, it becomes true when we build it.  The mind is a magic operator. Its scope cannot be given by a rule; the only reasonable approach is to believe that anything is possible; to believe in ourselves and others, beyond what any argument or theory can give. This assertion holds so easily, it can be tested, exactly as I am testing it now.

There is more than me in this test.  I have carried it around my whole life, Anything is possible. I want to know it, then, from you. I want to see you throw lightning into the world.