Snell's Law, Part The Second

{<−− Part I }                                                       {Part III  −−>}

Part 1 gives Snell's Law as a vector equation.   I have only accounted for a case in two dimensions, with N vertical in the plane.  Before going further, a little cleanup is necessary.  The initial diagram should be altered to match the solution, and I need to determine my relationship to a certain ± sign.

Time for a brief word about

VECTORS

■  A vector V is a line segment directed from a point a to another point b, written
           V = (b - a).
We subtract: tip − tail.   This subtraction (b - a) gives a new point, which I will call  v.  V can still be written as a difference of two points:
           V = (v − 0)
where 0 is the zero vector, which has all components zero. 
Hopefully, that sounds silly; subtracting zero doesn't do anything.  That is exactly what I want:

■ Any directed line segment is equivalent to a vector with the same direction and magnitude (length) whose tail is situated at the origin.
Example: Given points a = (a₁,  a₂) and b = (b₁, b₂)
        

Generalization:
■ All vectors with the same direction and magnitude, wherever they lie in space, are equivalent. 

■The Dot Product:  Given two vectors,  R = (r₁, r₂)  and   S = (s₁, s₂),
        
In three space, given  R= (r₁, r₂, r₃)  and  S = (s₁, s₂, s₃)
        

■ The result of the dot product is a regular-ass number (a scalar), not a vector.

■ The dot product of two normalized vectors gives the cosine of the angle between them.
Given  R = (cos α, sin α ),   S = (cosβ  , sinβ )
        
This is enough to evaluate the solution offered in Part 1:

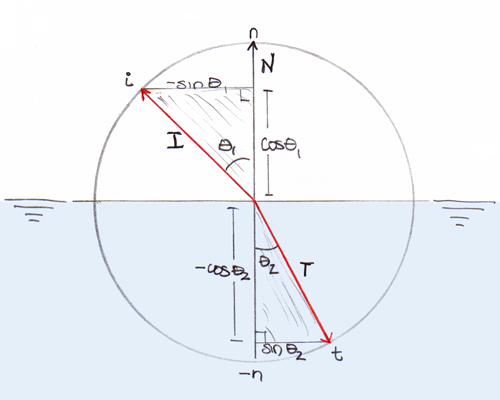
(Fig. 2)  - From Part 1 

Here again, the length of all vectors is 1.  The labeled points are then
        


The dashed line I' has the same direction and magnitude as I. Subtracting  tip − tail,
        

The two are the same.  But the angle between I' and N is  is (π − θ₁), not θ₁.  (Mouse over the image).
 Hence the angle between I and N  should also be (π − θ₁).  Is it?
        

Yes.   I want   I•N   to give cosθ₁, so I will change its direction:

(Fig. 3)  Corrected, N-Up

This is the correct diagram for the result in Part 1.  This is the definition of I that I used, and the formula should already be correct.

DEFAULT ORIENTATION

There is a trap waiting for me, and it's time to fall in.  The ± need to go.

What happens if the light comes from the other side?  In Fig. 3, what if I is on the right?  The mirrors of I and T share the same cosine.  The dot product does not distinguish between +θ and  −θ.   There are several ways to resolve this, which I am putting off to part 5.

I have chosen to set the default orientation in advance.  I've decided to cheat.  The computation of snell's law will happen in object space.  This is permitted by  a series of simplifying assumptions for real-time, which allow me to compute a reference plane once for the entire object:

1.  The surface in question is a sheet.
   It has a top side and a bottom side.  It is not necessarily flat and, for caustics, probably should not be.  Picutre a lake.
2. There is an up-direction.
    For a lake, on Earth, this is defined by gravity.  Air above, lake below.
3.   I will call the unit vector in this direction the reference normal, or the facing normal.  In local coordinate space I will  label it Z.
4. The reference normal can be in any direction in the game world.
   The lake can be upside down.  What matters is that the direction be defined.  Medium 1 will always lie on the positive side of the surface.  Specifically,
5. From the global coordinate space, the quadrant in which the light source lies, relative to the surface is already determined.

Example:
Pick any of the diagrams.  Place a boat on the surface of the water.   Now add waves.  The waves can pass freely through the diagram.  We could make a boat stability simulation: genetic algorithm builds boat, boat drops in water, waves pass through and rock the boat about.  A good boat does not sink.
In all of these cases, our 2D view stays put.  The surface normal changes as the waves pass through, but the air is always above, the water below.

To look at the boat from the side, we can rotate around it.  Of course, we leave the sky up, and the earth down.  The z-axis stays put.  This is the heart of my simplifying assumption.  I *think* it is why liquid surfaces are usually sheet meshes in a game engine, and not enclosed volumes.

I will not resolve the sign of θ for each ray. I will compute a Very Large Number of rays, rotate the surface, perform A Lot More, and so on.  I also believe this assumption will generalize further: I want to compute (fake) global lighting and caustics in rings at each point, using a MuchSmallerNumber of indiviual light paths.

FORMULA, N-UP:

Back to the diagram.  In this case,  the L is some positive angle less than 90 degrees from N.  I take the positive square root for sinθ₁; the first component of I is −sinθ₁, the first component of T  is (positive) sinθ₂, as shown in the diagrams.  And thus the formula:

This was actually the first formula I came up with.  Since I had peeked at the solution in the nVidia paper, I knew they had a ± I did not, and I backed up to recreate the difficulty which leads to its adoption.  I found it very instructive.  I had played around with the cross product and determinant, but still did not have a clear picture of how to resolve sign in a consistent manner, at different places in the transform.

{THIS IS ALL PRETEND}

I am making all of this up. I could be wrong about anything!  I could also be a seven-legged, scabby froodle.  But I'm a bit more worried about being
 Super
    Wrong.
Let me know!

{<−− Part I }                                                                {Part III  −−>} 

{CodeCogs does LaTeX equations for free.  Thanks, guys}