Preparing to to insure correct operation of the Dirac Delta in SAGE, if it has not already been fixed.
SUMS
■ (1.1)
■ (1.2)
■ (1.3)
■ If
(1.4)
Proof: {expand ↓}
This is saying the same thing twice, but the implications are not necessarily obvious.
Expand the sum over k in the right-hand side of (1.4)
![\small \sum_{k=a}^b x[k]\! \sum_{\lambda=a}^{b}h[\lambda] \,\;&=\;\, \left ( x[a] + x[a\!+\!1] + \ldots +x[b] \right ) \sum_{\lambda = a}^{b}h[\lambda]](http://latex.codecogs.com/gif.latex?\small \sum_{k=a}^b x[k]\! \sum_{\lambda=a}^{b}h[\lambda] \,\;&=\;\, \left ( x[a] + x[a\!+\!1] + \ldots +x[b] \right ) \sum_{\lambda = a}^{b}h[\lambda])
Separate individual terms of x[n]
![\small = x[a]\sum_{\lambda=a}^{b}h[\lambda] \;+\; x[a\!+\!1]\!\sum_{\lambda=a}^{b}h[\lambda] \;+\; \ldots \;+\; x[b]\sum_{\lambda=a}^{b}h[\lambda]](http://latex.codecogs.com/gif.latex?\small = x[a]\sum_{\lambda=a}^{b}h[\lambda] \;+\; x[a\!+\!1]\!\sum_{\lambda=a}^{b}h[\lambda] \;+\; \ldots \;+\; x[b]\sum_{\lambda=a}^{b}h[\lambda])
For each x[k], pull the corresponding term, h[λ=k] out of the summation
![\small \begin{align*} =\; &{\color{DarkBlue} x[a] h[a]} \,+\, x[a]\sum_{\lambda\ne a} h[\lambda] \\ &+ {\color{DarkBlue} x[a\!+\!1]h[a\!+\!1]} \,+\,x[a\!+\!1]\!\!\!\sum_{\lambda\ne a+1} \!\!\!h[\lambda]\\ &\;\;\;\;\;+\;\,\ldots\,\;+\; {\color{DarkBlue} x[b]h[b]} \,+\,x[b]\sum_{\lambda \ne b} h[\lambda]\;, \;\;\;\; \lambda = a \ldots b \end{align*}](http://latex.codecogs.com/gif.latex?\small \begin{align*} =\; &{\color{DarkBlue} x[a] h[a]} \,+\, x[a]\sum_{\lambda\ne a} h[\lambda] \\ &+ {\color{DarkBlue} x[a\!+\!1]h[a\!+\!1]} \,+\,x[a\!+\!1]\!\!\!\sum_{\lambda\ne a+1} \!\!\!h[\lambda]\\ &\;\;\;\;\;+\;\,\ldots\,\;+\; {\color{DarkBlue} x[b]h[b]} \,+\,x[b]\sum_{\lambda \ne b} h[\lambda]\;, \;\;\;\; \lambda = a \ldots b \end{align*})
Collecting like terms,
![\small = \sum_{k=a}^{b} {\color{DarkBlue} x[k]h[k]} \;+\; \sum_{k=a}^{b}x[k]\!\sum_{\lambda \ne k}\!h[\lambda],\;\; \lambda = a \ldots b](http://latex.codecogs.com/gif.latex?\small = \sum_{k=a}^{b} {\color{DarkBlue} x[k]h[k]} \;+\; \sum_{k=a}^{b}x[k]\!\sum_{\lambda \ne k}\!h[\lambda],\;\; \lambda = a \ldots b)
For (1.4) to be true, the second sum must be zero, which is the hypothesis, and the proof is complete.
Note: The individual terms in the sums are not prescribed. In general, there are an arbitrary number of nonzero terms in both summations. For example, choose three consecutive values of n. For
Σk x[k]h[k] = x1h1 + x2h2 + x3h3 = a,
the values of x1, x2, x3, which satisfy (1.4) for arbitrary values of h1, h2, h3, and a can be viewed as the solutions to the system
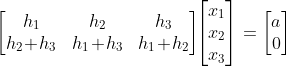
The general solution is
\nu}{h_1},\;\; x_2 = q-p\nu,\;\; x_3 = \nu)
where
-h_3(h_2\!+\!h_3)}{h_1(h_1\!+\!h_3)-h_2(h_2\!+\!h_3)},\;\; q= \frac{a(h_2\!+\!h_3)}{h_1(h_1\!+\!h_3)-h_2(h_2\!+\!h_3)})
and ν is an arbitrary scalar parameter.
Note: If we add the constrant 'every product must be zero whenever λ≠ k,' i.e.
![\small x[k]h[\lambda\! \ne \!k] = 0, \;\;\; k\!= a\ldots b,\; \lambda\! = a\ldots b](http://latex.codecogs.com/gif.latex?\small x[k]h[\lambda\! \ne \!k] = 0, \;\;\; k\!= a\ldots b,\; \lambda\! = a\ldots b)
there can be at most one nonzero term of the form x[k]h[k] in left hand side of (1.4). The consraint can be met for an arbitrary number of nonzero terms x[k]h[k] by introducing an auxiliary function. Any function which is zero everywhere but a single value of n will allow us to assign a one-to-one correspondence of our choice between k and λ.
Expand the sum over k in the right-hand side of (1.4)
Separate individual terms of x[n]
For each x[k], pull the corresponding term, h[λ=k] out of the summation
Collecting like terms,
For (1.4) to be true, the second sum must be zero, which is the hypothesis, and the proof is complete.
Note: The individual terms in the sums are not prescribed. In general, there are an arbitrary number of nonzero terms in both summations. For example, choose three consecutive values of n. For
Σk x[k]h[k] = x1h1 + x2h2 + x3h3 = a,
the values of x1, x2, x3, which satisfy (1.4) for arbitrary values of h1, h2, h3, and a can be viewed as the solutions to the system
The general solution is
where
and ν is an arbitrary scalar parameter.
Note: If we add the constrant 'every product must be zero whenever λ≠ k,' i.e.
there can be at most one nonzero term of the form x[k]h[k] in left hand side of (1.4). The consraint can be met for an arbitrary number of nonzero terms x[k]h[k] by introducing an auxiliary function. Any function which is zero everywhere but a single value of n will allow us to assign a one-to-one correspondence of our choice between k and λ.
DISCRETE MEASURE
■ Definition 1: The Dirac delta:
For discrete measure, this is also the unit impulse. For continuous measure, many functions behave as unit impulses.
■ Definition 2: The unit step:
■ Definition 3: THE CONVOLUTION SUM
■ (2.1)
Summation 1: By Definition 1, there is only one nonzero term of δ[λ], at λ = 0. If n < 0, the sum is 0; if n ≥ 0, the sum is 1. This is the definition of u[n].
Summation 2 follows immediately from the substitution k = n − λ.
■ (2.2) Summation 2 follows immediately from the substitution k = n − λ.
■ (2.3)
This is equivalent to the dot product of two vectors, x and h, whose components are the x[k] and h[λ], respectively, in counting order a . . . b.
■ (2.4)
I will work with bounded summations. These bounds can be lifted at any time, and the general case (all summations from −∞ to +∞, for all n) holds.
■ Definition 4: The nonzero range of x[n] is the smallest interval covering all nonzero values of x[n].
- The range may be finite or infinte.
-
x[n] may be zero inside the interval: we may have
x[c] = 0, for some or all c, a < c < b.
Only the endpoints [a,b] must be nonzero, {and only if the interval is finite. ??} - x[n] must be identically zero outside the interval (by definition).
- We may have a = b. This is the case with δ[n], whose nonzero range is [0,0].
-
The number of points in the nonzero range is b − a + 1.
For example, δ[n] has 0-0+1 = 1 point. - {I am making this up so please let me know if you have preferred notation conventions. I just want to establish ranges.}
___________
■ In the following summations, x[n], h[n] and g[n] have finite nonzero rangesx[n] : a ≤ n ≤ b
h[n]: c ≤ n ≤ d
g[n]: e ≤ n ≤ f
___________
■ Let a ≤ n ≤ b be the nonzero range of x[n]. Then
(2.5)
Proof: {expand ↓}
δ[n − k] is nonzero only when k = n, so ![\inline \sum_{k\ne n} x[k]\delta[n-k] \,=\, 0](http://latex.codecogs.com/gif.latex?\inline \sum_{k\ne n} x[k]\delta[n-k] \,=\, 0) . Now consider the summation for a fixed value of n, ni. If a ≤ ni ≤ b, then exactly one of these terms is nonzero and it occurs when k = ni:
. Now consider the summation for a fixed value of n, ni. If a ≤ ni ≤ b, then exactly one of these terms is nonzero and it occurs when k = ni:
![\small \small \begin{align*} \sum_{k=a}^{b}x[k]\delta[n_i\!-\!k] \;&=\; x[a]\delta[n_i\!-\!a] \,+\, x[a\!+\!1]\delta[n_i\!-\!(a\!+\!1)] \,+\, \ldots \, +\, x[b]\delta[n_i\!-\!b]\\ &=\; x[n_i]\delta[n_i - n_i] \;\;\;=\;\;\; x[n_i]\delta[0]\\ & =\; x[n_i] \end{align*}](http://latex.codecogs.com/gif.latex?\small \small \begin{align*} \sum_{k=a}^{b}x[k]\delta[n_i\!-\!k] \;&=\; x[a]\delta[n_i\!-\!a] \,+\, x[a\!+\!1]\delta[n_i\!-\!(a\!+\!1)] \,+\, \ldots \, +\, x[b]\delta[n_i\!-\!b]\\ &=\; x[n_i]\delta[n_i - n_i] \;\;\;=\;\;\; x[n_i]\delta[0]\\ & =\; x[n_i] \end{align*})
For all n: a ≤ n ≤ b.
If n is outside the range a ≤ n ≤ b, there is no k = ni and every term is zero.
i.e.![\small \sum_{k=a}^b x[k]\delta[n\!-\!k] = 0](http://latex.codecogs.com/gif.latex?\small \sum_{k=a}^b x[k]\delta[n\!-\!k] = 0) for n < a, n > b.
for n < a, n > b.
For all n: a ≤ n ≤ b.
If n is outside the range a ≤ n ≤ b, there is no k = ni and every term is zero.
i.e.
■ (2.6)
x[n] offset by an arbitrary constant.
■ (2.7)
The sums are zero outside the range k + c ≤ n ≤ k + d
Alternately, the constant bounds of the range are a + c ≤ n ≤ b + d
■ (2.8) Alternately, the constant bounds of the range are a + c ≤ n ≤ b + d
■ COMMUTATIVE:
■ ASSOCIATIVE:
The nonzero range of the convolution is k + λ + e ≤ n ≤ k + λ + f
Proof: {expand ↓}
Beginning on the right-hand side, let
w[n] = x[n] * h[n],
v[n] = h[n] * g[n]
Then
![\small (x[n]*h[n])*g[n] \; =\; w[n]*g[n] \;= \sum_{i = -\infty}^{+\infty}\!\!w[i]g[n-i]](http://latex.codecogs.com/gif.latex?\small (x[n]*h[n])*g[n] \; =\; w[n]*g[n] \;= \sum_{i = -\infty}^{+\infty}\!\!w[i]g[n-i])
Where![\small w[i] = \sum_{k=a}^{b}x[k]h[i-k]](http://latex.codecogs.com/gif.latex?\small w[i] = \sum_{k=a}^{b}x[k]h[i-k]) . Hence,
. Hence,
(A)![\small \sum_{i=-\infty}^{+\infty}\!\!w[i]g[n\!-\!i] \;= \sum_{i=-\infty}^{+\infty}\sum_{k=a}^{b}x[k]h[i\!-\!k]g[n\!-\!i]](http://latex.codecogs.com/gif.latex?\small \sum_{i=-\infty}^{+\infty}\!\!w[i]g[n\!-\!i] \;= \sum_{i=-\infty}^{+\infty}\sum_{k=a}^{b}x[k]h[i\!-\!k]g[n\!-\!i]) .
.
The nonzero range of g[n] is e ≤ n ≤ f. Expanding g[n−i], the right-hand side of (A) becomes
(B)![\small \sum_{k=a}^{b}x[k]\!\! \sum_{i=-\infty}^{+\infty}\!\! h[i\!-\!k] \sum_{m=e}^{f}g[m]\delta[n\!-\!m\!-\!i]](http://latex.codecogs.com/gif.latex?\small \sum_{k=a}^{b}x[k]\!\! \sum_{i=-\infty}^{+\infty}\!\! h[i\!-\!k] \sum_{m=e}^{f}g[m]\delta[n\!-\!m\!-\!i]) .
.
The nonzero ranges of h[n] is c ≤ n ≤ d. Expanding h[i−k] gives
(C)![\small \sum_{k=a}^{b}x[k]\!\! \sum_{i=-\infty}^{+\infty} \sum_{\lambda=c}^d h[\lambda]\delta[i\!-\!k\!-\!\!\lambda] \sum_{m=e}^{f}g[m]\delta[n\!-\!i\!-\!m]](http://latex.codecogs.com/gif.latex?\small \sum_{k=a}^{b}x[k]\!\! \sum_{i=-\infty}^{+\infty} \sum_{\lambda=c}^d h[\lambda]\delta[i\!-\!k\!-\!\!\lambda] \sum_{m=e}^{f}g[m]\delta[n\!-\!i\!-\!m]) .
.
δ[i − k − λ] ≠ 0 only when i = k + λ. Both λ and k are constant for summation over i, and (C) =
(D)![\sum_{k=a}^{b}x[k] \sum_{\lambda=c}^d h[\lambda] \sum_{m=e}^{f}g[m]\delta[n\!-\!k\!-\!\lambda\!-\!m]](http://latex.codecogs.com/gif.latex?\sum_{k=a}^{b}x[k] \sum_{\lambda=c}^d h[\lambda] \sum_{m=e}^{f}g[m]\delta[n\!-\!k\!-\!\lambda\!-\!m]) .
.
δ[n − k − λ − m] is nonzero only when m = n − k − λ, and (D) =
(E)![\sum_{k=a}^{b}x[k] \sum_{\lambda=c}^d h[\lambda] g[n\!-\!k\!-\!\lambda]](http://latex.codecogs.com/gif.latex?\sum_{k=a}^{b}x[k] \sum_{\lambda=c}^d h[\lambda] g[n\!-\!k\!-\!\lambda]) .
.
The sum is zero outside the range (k + λ + e) ≤ n ≤ (k + λ + f).
Lastly, consider the left-hand convolution
![\small x[n]*(h[n]*g[n]) \; =\; x[n]*v[n] \;=\; \sum_{k = a}^{b}x[k]v[n-k]](http://latex.codecogs.com/gif.latex?\small x[n]*(h[n]*g[n]) \; =\; x[n]*v[n] \;=\; \sum_{k = a}^{b}x[k]v[n-k])
where, by (2.8)![\small v[n\!-\!k] \;=\; \sum_{\lambda=c}^{d}h[\lambda]g[n\!-\!k\!-\!\lambda]](http://latex.codecogs.com/gif.latex?\small v[n\!-\!k] \;=\; \sum_{\lambda=c}^{d}h[\lambda]g[n\!-\!k\!-\!\lambda]) . Hence,
. Hence,
(F)![\small \sum_{k=a}^{b}x[k]v[n\!-\!k] \;=\; \sum_{k=a}^{b}x[k]\sum_{\lambda=c}^{d}h[\lambda]g[n\!-\!k\!-\!\lambda]](http://latex.codecogs.com/gif.latex?\small \sum_{k=a}^{b}x[k]v[n\!-\!k] \;=\; \sum_{k=a}^{b}x[k]\sum_{\lambda=c}^{d}h[\lambda]g[n\!-\!k\!-\!\lambda]) .
.
(F) = (E), and the circuit is complete.
The equalities are easier to derive without using δ[n]. For example, from (A), substitute λ = i − k, and immediately
![\small \begin{align*} \sum_{k=a}^{b} x[k]\!\!\!\!\! \sum_{\;\;\lambda=-k-\infty}^{-k+\infty}\!\!\!\!\!\!h[\lambda]g[n\!-\!k\!-\!\lambda] \;=\; \sum_{k=a}^{b} x[k] \sum_{\;\;\lambda=c}^{d}\!h[\lambda]g[n\!-\!k\!-\!\lambda] \end{align*}](http://latex.codecogs.com/gif.latex?\small \begin{align*} \sum_{k=a}^{b} x[k]\!\!\!\!\! \sum_{\;\;\lambda=-k-\infty}^{-k+\infty}\!\!\!\!\!\!h[\lambda]g[n\!-\!k\!-\!\lambda] \;=\; \sum_{k=a}^{b} x[k] \sum_{\;\;\lambda=c}^{d}\!h[\lambda]g[n\!-\!k\!-\!\lambda] \end{align*})
{Should SAGE eliminate δ[n] whenever possible? Only when asked to simplify? .... Best practices?
Homework: Dissect the existing Convolution code.}
w[n] = x[n] * h[n],
v[n] = h[n] * g[n]
Then
Where
(A)
The nonzero range of g[n] is e ≤ n ≤ f. Expanding g[n−i], the right-hand side of (A) becomes
(B)
The nonzero ranges of h[n] is c ≤ n ≤ d. Expanding h[i−k] gives
(C)
δ[i − k − λ] ≠ 0 only when i = k + λ. Both λ and k are constant for summation over i, and (C) =
(D)
δ[n − k − λ − m] is nonzero only when m = n − k − λ, and (D) =
(E)
The sum is zero outside the range (k + λ + e) ≤ n ≤ (k + λ + f).
Lastly, consider the left-hand convolution
where, by (2.8)
(F)
(F) = (E), and the circuit is complete.
The equalities are easier to derive without using δ[n]. For example, from (A), substitute λ = i − k, and immediately
{Should SAGE eliminate δ[n] whenever possible? Only when asked to simplify? .... Best practices?
Homework: Dissect the existing Convolution code.}
■ DISTRIBUTIVE:
Proof: {expand ↓}
■ Considerations:
If x[n] is unknown or undefined outside the range a ≤ n ≤ b, should we treat it as zero? I believe this is consistent with user expectations for audio and image processing. {Am I off base here?}
Examples:
Signal envelopes: beyond the bounds of the envelope we tacitly assume the function carries on infinitely in both directions, with a value of zero
Finite recordings: beyond the head and tail, there is "no signal", i.e. x(t) = 0.
Image boundaries.
For practical computation, functions which are zero outside given ranges can be defined internally following (2.5). Say, for example, by
![x[n] = \left\{ \begin{matrix} \sum_{k=a}^{b}x[k]\delta[n-k], & a\le n\le b, & k=n\\ 0, &\mathrm{otherwise} \end{matrix}\right.](http://latex.codecogs.com/gif.latex?x[n]%20=%20\left\{%20\begin{matrix}%20\sum_{k=a}^{b}x[k]\delta[n-k],%20&%20a\le%20n\le%20b,%20&%20k=n\\%200,%20&\mathrm{otherwise}%20\end{matrix}\right.)
without loss of generality. They can be displayed as infinite summations when desired or appropriate.
{Please correct me!}
Examples:
Signal envelopes: beyond the bounds of the envelope we tacitly assume the function carries on infinitely in both directions, with a value of zero
Finite recordings: beyond the head and tail, there is "no signal", i.e. x(t) = 0.
Image boundaries.
For practical computation, functions which are zero outside given ranges can be defined internally following (2.5). Say, for example, by
without loss of generality. They can be displayed as infinite summations when desired or appropriate.
{Please correct me!}
■ WARNING:
1) These expressions assume the data exist, and are everywhere zero outside the nonzero range of x[n].
Summing in this way is not in general efficient; the sums may contain an arbitrary number of unnecessary (zero) terms within the total nonzero range.
2) The sums do not enforce zero values.
The nonzero range of the convolution x[n]*h[n] is not the same as that of x[n] or h[n] alone. In the above sums, x[n] and h[n] are sampled over the total length of the convolution. This may include an arbitrary number of terms of both functions which are assumed zero.
These convolution sums do not discard terms which are assumed zero, but inside the nonzero range.
To insure that no terms which are assumed zero are included in the summation, it must be broken up into piecewise intervals.
Summing in this way is not in general efficient; the sums may contain an arbitrary number of unnecessary (zero) terms within the total nonzero range.
2) The sums do not enforce zero values.
The nonzero range of the convolution x[n]*h[n] is not the same as that of x[n] or h[n] alone. In the above sums, x[n] and h[n] are sampled over the total length of the convolution. This may include an arbitrary number of terms of both functions which are assumed zero.
These convolution sums do not discard terms which are assumed zero, but inside the nonzero range.
To insure that no terms which are assumed zero are included in the summation, it must be broken up into piecewise intervals.