THE SUM OF TWO PERIODIC FUNCTIONS
Given two elementary periodic functions,When is the sum
1. WHEN IS THE SUM PERIODIC?
fi(t) is periodic with period Ti= 1/ci
fj(t) is periodic with period Tj = 1/cj
If the sum is periodic then there exist two integers k1, k2 such that

That is, some multiple of Ti is also a multiple of Tj. Take two tires, place them next to each other. Mark a vertical lines down the side of each tire. Now spin them at two different speeds, 2πci and 2πcj. If those two lines are ever vertical at the same time in the future, then each wheel has at that moment completed a revolution. For the tire fi this is the k1th revolution. For the the tire fj this is the k2th revolution.
If no such integers exist, the sum is not periodic. Putting the k's on one side:

So we have a simple rule:
If Ti/Tj is irrational, then there are no such k1, k2 and y(t) is not periodic.
2-1. DETERMINE THE PERIODfj(t) is periodic with period Tj = 1/cj
If the sum is periodic then there exist two integers k1, k2 such that
That is, some multiple of Ti is also a multiple of Tj. Take two tires, place them next to each other. Mark a vertical lines down the side of each tire. Now spin them at two different speeds, 2πci and 2πcj. If those two lines are ever vertical at the same time in the future, then each wheel has at that moment completed a revolution. For the tire fi this is the k1th revolution. For the the tire fj this is the k2th revolution.
If no such integers exist, the sum is not periodic. Putting the k's on one side:
So we have a simple rule:
If Ti/Tj is irrational, then there are no such k1, k2 and y(t) is not periodic.
If we can find on pair k1, k2 then we can find an infinite number of them: multiply both sides by some integer n:
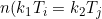)
nk1, nk2 are integers which satisfy our query. To determine the fundamental period of y(t), we seek the least integers that satisfy k1, k2. I'll do this by reducing fractions as I work. In short,
■ Procedure: Given
 = \sin(2\pi \tfrac{m}{r}t) + \sin(2\pi\tfrac{n}{s}t), \;\;\;\;\; m, r, n, s \;\; \textup{integer})
1. Reduce m/r and n/s to lowest terms: M/R, N/S.
2. Set c1= the greatest common factor of the numerators M and N.
c2 = the greatest common factor of the denominators R and S.
Then y(t) is periodic with period
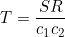
2-2. THE DETAILS:nk1, nk2 are integers which satisfy our query. To determine the fundamental period of y(t), we seek the least integers that satisfy k1, k2. I'll do this by reducing fractions as I work. In short,
■ Procedure: Given
1. Reduce m/r and n/s to lowest terms: M/R, N/S.
2. Set c1= the greatest common factor of the numerators M and N.
c2 = the greatest common factor of the denominators R and S.
Then y(t) is periodic with period
Introduce positive integers m, n, r, s;
Rational numbers P = m/r, Q = n/s;
Distinct irrational numbers φ, θ. (with all rational factors removed)
Reduce m/r and n/s (remove common factors, if any), and let
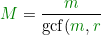}, \;\;\;\;\; {\color{DarkGreen} R} = \frac{{\color{DarkGreen} r}}{\mathrm{gcf}({\color{DarkGreen} m},{\color{DarkGreen} r})}, \;\;\;\;\; {\color{DarkGreen} N} = \frac{{\color{DarkGreen} n}}{\mathrm{gcf}({\color{DarkGreen} n},{\color{DarkGreen} s})}, \;\;\;\;\; {\color{DarkGreen} S} = \frac{{\color{DarkGreen} s}}{\mathrm{gcf}({\color{DarkGreen} n},{\color{DarkGreen} s})})
Expressed as fractions in lowest terms,

Introduce elementary periodic functions fi(t), and corresponding periods Ti:
 = \sin(2\pi {\color{DarkGreen} m} t), \;\;\;\;\; T_1 =\; 1/{\color{DarkGreen}m}\\ &f_2(t) = \sin(2\pi {\color{DarkGreen} n} t ), \;\;\;\;\;\; T_2 =\; 1/{\color{DarkGreen}n} \end{align*})
 = \sin(2\pi {\color{Blue} P} t), \;\;\;\;\; T_3 = 1/{\color{Blue}P} =\; {\color{DarkGreen}R}/{\color{DarkGreen}M}\\ &f_4(t) = \sin(2\pi {\color{Blue} Q} t ), \;\;\;\;\; T_4 = 1/{\color{Blue}Q} =\; {\color{DarkGreen}S}/{\color{DarkGreen}N}\\ \end{align*})
 = \sin(2\pi {\color{Blue}P}{\color{Orange} \phi} t), \;\;\;\;\; T_5 = \frac{1}{{\color{Blue}P}{\color{Orange}\phi}} =\; \frac{{\color{DarkGreen}R}}{{\color{DarkGreen}M}{\color{Orange}\phi}}\\ &f_6(t) = \sin(2\pi {\color{Blue}Q}{\color{Orange} \theta} t), \;\;\;\;\; T_6 = \frac{1}{{\color{Blue}Q}{\color{Orange}\theta}} =\; \frac{{\color{DarkGreen}S}}{{\color{DarkGreen}N}{\color{Orange}\theta}} \end{align*})
Determine the period of y(t), for the following periods of the f(t). Rational numbers P = m/r, Q = n/s;
Distinct irrational numbers φ, θ. (with all rational factors removed)
Reduce m/r and n/s (remove common factors, if any), and let
Expressed as fractions in lowest terms,
Introduce elementary periodic functions fi(t), and corresponding periods Ti:
(a) Integer periods.
Let  = f_1(t) + f_2(t)) .
.
The fundamental period is given by the least integers k1, k2 such that:
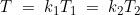
We have
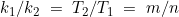
Remove common factors of m and n:
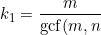}\,, \;\;\;\;\; k_2 = \frac{n}{\mathrm{gcf}(m,n)})
Using T = k1T1 . . . y(t) is periodic with period
})
(b) Rational periods. The fundamental period is given by the least integers k1, k2 such that:
We have
Remove common factors of m and n:
Using T = k1T1 . . . y(t) is periodic with period
Let  = f_3(t) + f_4(t)) .
.
If y(t) is periodic, there are integers k1 and k2 such that T = k1T3 = k2T4.
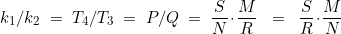
To put k1/k2 in lowest terms, reduce S/R and M/N. (S/N and M/R are already reduced).
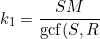\mathrm{gcf}(M,N)}, \;\;\;\;\; k_2 = \frac{RN}{\mathrm{gcf}(S,R)\mathrm{gcf}(M,N)})
Using T = k1T3, . . . y(t) is periodic with period
\mathrm{gcf}(M,N)})
(c) One signal irrational. If y(t) is periodic, there are integers k1 and k2 such that T = k1T3 = k2T4.
To put k1/k2 in lowest terms, reduce S/R and M/N. (S/N and M/R are already reduced).
Using T = k1T3, . . . y(t) is periodic with period
Let  = f_4(t)+f_5(t)) .
.
We know that the ratio of periods cannot be rational. y(t) is not periodic.
Specifically, we must have
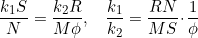
But φ didn't stop being irrational. There are no such k1, k2.
(d) Both signals irrationalWe know that the ratio of periods cannot be rational. y(t) is not periodic.
Specifically, we must have
But φ didn't stop being irrational. There are no such k1, k2.
Let  = f_5(t)+f_6(t)) .
.
If φ and θ were multiples of the same common irrational number, then the sum is still periodic. (In the examples above, all coefficients of t have the common factors 2 and π. This does not affect whether or not their sums are periodic.)
θ and φ are distinct rational numbers; f5(t) + f6(t) is not periodic.
If φ and θ were multiples of the same common irrational number, then the sum is still periodic. (In the examples above, all coefficients of t have the common factors 2 and π. This does not affect whether or not their sums are periodic.)
θ and φ are distinct rational numbers; f5(t) + f6(t) is not periodic.
■Next Question: At what time tm does the maximum value of y(t) occur?