The geometric mean of n positive numbers is less than the arithmetic mean.
(Except when all n numbers are the same, in which case the two means are equal)
■ The Arithmetic Mean — Add n numbers together, and divide by n:
■ The Geometric mean — Multiply n numbers, and take the nth root:
In symbols, Cauchy's mean theorem states
The equal condition can be omitted as long as a, b, c, ... n are not all identical.
This is problem #10 in 100 Great Problems of Elementary Mathematics. Dörrie holds the sum constant and examines the product, so for practice I'll go in the reverse direction. Suppose we have two positive numbers x and y, with x > y. If the product xy is kept constant, what happens to the two means as x and y are brought closer together?
Introduce a new number a which satisfies
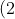\;\;\;\;\;\;\;\;\;\; x \,>\, \frac{x}{a}\,\ge\, ay\,> \,y "(2)Two pairs; (x,y) and (x/a, ay)")
The two new numbers, (x/a) and (ay) are sandwiched between x and y. Their product is constant and the same as xy:
(ay)\; = \;xy "The two products are equal.")
What values of a satisfy (2)? Evaluating each inequality sign separately gives the range of a:
\;\;\;\;\;\;\;\;\; \left.\begin{matrix} \;\; x\, > x/a, &\;\;a > 1 \\ \;\;\;\; ay > y, \;\;\;\;\;\; &\;\;a > 1 \\ \; x/a \ge ay, \;\;\; &\sqrt{x/y} \ge a \;\; \end{matrix}\right\}\;\;\;\; 1 < a \le \sqrt{x/y} "(3) The range of a")
According to Cauchy's theorem, two properties should be satisfied by a. First, I should always have
(4.1) ½(x/a+ay) > √xy,
except when x/a = ay. Second when a = √ x/y, then x/a = ay, and the geometric and arithmetic mean of this number will be the same.
Aha! I arrive at the same place Dörrie found himself: it is easier to prove a somewhat stronger result. Instead of untangling (4.1), suppose I say,
\;\;\;\;\;\;\;\;\;\; \begin{align*} x-\!\frac{x}{a} &> ya\! - \!y \;\;\;\therefore \;\;\; x + y \,> \,ya + \frac{x}{a} \end{align*} "(4)The minimum value for the arithmetic mean occurs when the two numbers are equal")
If the left side is true, then the right is true. But the right side says,
/a \; > \; y(a\!-\!1), \;\;\;\;\; \boldsymbol{x > ay} "(4) is true")
Yes. Skipping to the second property, let the distance x/a − ay go to zero. This is the maximum value of a. Are both the geometric and arithmetic mean of this number the same? Let a = √ x/y. Then
\;\;\;\;\;\;\;\begin{align*} &M \,= \frac{1}{2}\!\left(\frac{x}{a} + \!ya \right ) \,=\, \frac{1}{2}\!\!\left( \frac{x\sqrt{y}}{\sqrt{x}} + \!\frac{y\sqrt{x}}{\sqrt{y}}\right) \,=\, \sqrt{xy}\\ &\mathfrak{M} \,=\, \sqrt{\frac{x}{a}(ay)} \;=\, \sqrt{xy} \end{align*} "5. The two means")
Yes.
Using the same procedure, the result can be extended to n numbers. Given a product P = xyz . . . n, suppose not all the numbers are equal. Choose any two numbers u ≠ v. For convenience, I choose the largest and smallest values. Reduce the difference (u-v) to zero as above, replacing both u and v with w = √ uv. The product of n numbers is the same; their sum reduced, as above.
Repeat until all the numbers are identical, always choosing the greatest and least numbers. Each step reduces the sum (and therefore the Arithmetic mean) and eliminates one difference among the n values. The product P is constant. When all the numbers are identical, there is no longer a greatest and least element. The arithmetic mean of this sequence is
nα/n = α and the geometric mean is
α n/n = α
Thus, for any sequence of numbers xyz . . . n of constant product P the minimum value of the arithmetic mean is achieved when the numbers are identical. This number is the geometric mean of the original n numbers.1
Since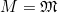
only when M is minimum, and 
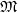held constant, the result follows:
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \sqrt[\boldsymbol{n}]{a \cdot b \cdot c \;\cdots\;} \;\; \le \;\; \frac{a+b+c+ \cdots }{n} "(1) Cauchy's Mean Theorem (again)")
which is Cauchy's mean Theorem. Now, suppose we replace a, b, c . . . however we wish, as long as their sum remains the same. The right hand remains constant, and the left varies. The two will be equal only when a, b, c . . . n are the same number. Then
a, a, . . . , a, 1, 1, . . . , 1 a > 0, a ≠ 1
There are n a's and (m − n) 1's. The two means are:
}{m} \; =\; \frac{n}{m}(a\!-\!1) + 1 \\ \mathfrak{M}\; &=\;\;\; \sqrt[m]{a^n \cdot 1^n} \;\;\;\; = \;\;\;\;\; \sqrt[m]{a^n} \end{align*} "The two means")
Since a ≠ 1, the numbers are not all equal, and therefore
 + 1 "GeoM < ArithM")
Substituting λ for n/m gives
\;\;\;\;\;\;\;\;\;\; a^\lambda \; < \; \lambda(a\!-\!1) + 1, \;\;\;\;\;\;\; 0< \lambda< 1 "(6) Exponential Inequality, c < 1")
For λ > 1, flip the inequality.
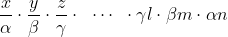
and on the next pass there remain (at most) n/4 distinct intervals... and so on. Regardless of the procedure, we close in on the same number. Is there a good way to estimate square roots hiding in here?
Introduce a new number a which satisfies
The two new numbers, (x/a) and (ay) are sandwiched between x and y. Their product is constant and the same as xy:
What values of a satisfy (2)? Evaluating each inequality sign separately gives the range of a:
According to Cauchy's theorem, two properties should be satisfied by a. First, I should always have
(4.1) ½(x/a+ay) > √xy,
except when x/a = ay. Second when a = √ x/y, then x/a = ay, and the geometric and arithmetic mean of this number will be the same.
Aha! I arrive at the same place Dörrie found himself: it is easier to prove a somewhat stronger result. Instead of untangling (4.1), suppose I say,
If the left side is true, then the right is true. But the right side says,
- Auxiliary Theorem: Given two pairs of numbers with the same product, the pair that is closer together will always have the smaller sum.
Yes. Skipping to the second property, let the distance x/a − ay go to zero. This is the maximum value of a. Are both the geometric and arithmetic mean of this number the same? Let a = √ x/y. Then
Yes.
Using the same procedure, the result can be extended to n numbers. Given a product P = xyz . . . n, suppose not all the numbers are equal. Choose any two numbers u ≠ v. For convenience, I choose the largest and smallest values. Reduce the difference (u-v) to zero as above, replacing both u and v with w = √ uv. The product of n numbers is the same; their sum reduced, as above.
Repeat until all the numbers are identical, always choosing the greatest and least numbers. Each step reduces the sum (and therefore the Arithmetic mean) and eliminates one difference among the n values. The product P is constant. When all the numbers are identical, there is no longer a greatest and least element. The arithmetic mean of this sequence is
nα/n = α and the geometric mean is
α n/n = α
Thus, for any sequence of numbers xyz . . . n of constant product P the minimum value of the arithmetic mean is achieved when the numbers are identical. This number is the geometric mean of the original n numbers.1
Since
which is Cauchy's mean Theorem. Now, suppose we replace a, b, c . . . however we wish, as long as their sum remains the same. The right hand remains constant, and the left varies. The two will be equal only when a, b, c . . . n are the same number. Then
- Auxiliary Theorem 2: For n numbers of constant sum, the geometric mean reaches its maximum value when all n numbers are the same.
EXPONENTIAL INEQUALITY
Consider a sequence of m numbers, n of which have the positive value a, and the rest equal to one:a, a, . . . , a, 1, 1, . . . , 1 a > 0, a ≠ 1
There are n a's and (m − n) 1's. The two means are:
Since a ≠ 1, the numbers are not all equal, and therefore
Substituting λ for n/m gives
For λ > 1, flip the inequality.
■
...whence, upon having been put into the box and acquiring thereby the passive tense to which the greater part of his misery was owing and, that part outweighing the joyful to such a degree that of the expression relating the two it was conjectured the mathematics were differential with his share of joy -alas!- the quantity to be driven to zero, he began at that precise moment to conjecture it would be his ultimate undoing (for so it was conjectured about him and therefore & c.), and so entraining the drowsy progressive he then began to conjecture that it would not be his ultimate undoing, whereupon the fueling and fanning, oiling and wiping bringing to bear an ever increasing velocity to the transit of time, each passing second closing yet further betwixt gerund and he the gap, at last the imperfect arrived,
he undid it and freed himself.
It was still two weeks before he would be let out of the box.
_______________________________________________________
1There are other, more efficient ways to arrive at the same result. For example the sequence can be treated as (at most) n/2 different, nested intervals like this:and on the next pass there remain (at most) n/4 distinct intervals... and so on. Regardless of the procedure, we close in on the same number. Is there a good way to estimate square roots hiding in here?
No comments:
Post a Comment