The Elements, Book I (Prop I - V)

The Thirteen Books of the Elements

Euclid


Book I

Reference edition: Sir Thomas Heath, Johan Ludvig Heiberg
 The University Press, 1908

Free Google Ebook

Proposition I:  Given finite straight line AB, to construct an equilateral triangle.

Proposition II:  To place at a given point a straight line equal to a given straight line.

Given point A and straight line BC,

Construct equilateral triangle ΔABD [Prop. I]

Construct the circle with center B, and radius BC.

Extend the straight line DB to intersect the circle.  Call the point of intersection F
BC ≅ BF

Construct the circle with center D and radius DF.

Extend straight line DA to intersect this new circle.  Call the point of intersection G:

Now, DG ≅ DF

and AD ≅ BD
And therefore DG − AD ≅ DF − BD
But DG − AD = AG
and DF − BD = BF
Hence AG ≅ BF.

Proposition III:  Given two unequal straight lines, to cut off from the greater a straight line equal to the lesser.

Given straight line AB (the greater) and straight line C (the lesser),

Use an endpoint of C to draw a circle of radius C.

Connect A to the endpoint and build an equilateral triangle. (Prop I)
Extend the side of the triangle to the circle. (Prop II)

Draw a second circle with center at D and extend DA to intersect the circle. (Prop II)

Draw a third circle with center A which also intersects this point:

The intersection of this last circle with AB is labeled γ.
Aγ ≅ C and the construction is complete.

Proposition IV: Side-Angle-Side Congruence

If you can find more than one way to draw the segment BC, let me know.

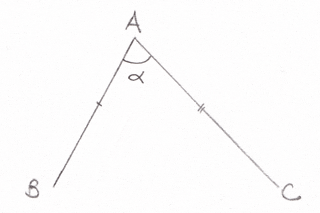
Proposition V: In an isosceles triangle, the base angles are equal.  If the equal sides are extended in straight lines, the angles under the base are equal.

Given  AB

Construct AC = AB and isosceles triangle ΔABC.

Construct AC = AB and isosceles triangle ΔABC.
Extend AB  to arbitrary point F.
Place  CG = BF  [Prop II, or by definition with the compass]

Connect   FC, GB
     ΔFCA ≅ ΔGBA  [Prop IV, common angle ∠A]
The corresponding angles and sides are then equal, namely
     FC = GB,    ∠CFA ≅ ∠BGA

Then ΔFCB ≅ ΔGBC and
     ∠FBC = ∠GCB,   (the angles under the base)
     ∠BCF = ∠CBG
And  ∠ABC  = ∠ABG −∠CBG  = ∠ACF − ∠BCF  = ∠ACB (the base angles of the isosceles triangle)
Which were the things to be proved.

{Next −−>}

____________________________________
There are hundreds of propositions remaining of which I will post a selection, including only a restatement of the Proposition and a completed diagram.