There are two basic kinds of microphones. A
Pressure microphone is open to the environment on one side. The closed side of the diaphragm faces an enclosed volume of air. Pressure changes on the open side are measured against the closed reference. Such a microphone is
omnidirectional: it is insensitive to
angular changes in sound pressure. A change in instantaneous pressure on one side moves the diaphragm. Forces arriving at different angles, but which produce identical instantaneous pressure are recorded identically.
In a
Pressure Gradient microphone, the diaphragm is open on both sides. The pickup pattern is a
figure-8. There is no reference volume for forces arriving off the axis of the diaphgram: equal forces in opposite directions cancel and the component of force in the direction perpendicular to the diaphgram is always zero, irrespective of the magnitude of the force.
The gradient microphone records the component of force in the direction of its axis.
It experiences a phase difference in sound pressure.
A pressure mic can be combined with a gradient mic to create a directional microphone with a cardioid pattern:
FIG1 Adding Capsules
FIG1
General equations for the omnidirectional microphone is
Omni : r = a
Figure-8: r = b cos θ {Cartesian: (x-b/2)
2 + y
2 = (b/2)
2}
1. Cardioid = Omni + Gradient:
(1) r
c = a + b cos
θ = Mid
The classic cardioid is produced when the two circles are tangent; when a = b :
(1b) r
c = a(1+cos
θ)
In a Mid-Side recording, this is the Mid microphone.
2. Stereo = Cardioid ± Gradient (figure-8):
(2L) r
L = a + b cosθ + c sin
θ = Mid + Side
(2R) r
R = a + b cos
θ − c sin
θ = Mid − Side
where
a,
b,
c. are arbitrary positive constants.
The second (Side) microphone is perpendicular to the axis of the cardioid. In other words,
Mid-Side recording (perpendicular figure-8's + omni) is a stereo field (a Blumelein pair) with an oreintation provided by the omni capsule.
These are precisely the preliminary conditions we require for an orientable image. Note that a Blumelein pair is insufficient; it lacks an orientation.
To compare different stereo recording methods, and transform them as spatial images, I need a series of reference points.
Reference Microphone and Level: Use a cardioid (directional) microphone as a frame of reference, with a polar pattern normalized to r=1 in the direction of maximum sensitivity.
(I may switch to using a reference
area.)
The maximum value of (1)
is
a +
b. Hence a = 1 − b, and
(1)' r
c = 1 + b(cos
θ −1), 0 ≤ b ≤ 1
b interpolates between omnidirectional (
b=0) and figure-8 (b=1). The classic cardioid occurs at b = ½.
We now have for Stereo (2) :
(2)' r
L,R = 1 + b(cos
θ −1) ± c sin
θ
r
L and r
R are symmetric about the facing vector. The matrix <M+S, M−S> = <L, R> represents two cardioid patterns rotated in ±θ respectively. As
c increases from 0 (no Side channel), M + S rotates toward 90°, but won't reach it unless b=0. For r
L, all values of sin, cos are positive.
Stereo Width:
Let θ
1 denote the angle of maximum sensitivity implied by L. r
L is maximum when
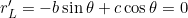
, and
r ≠ 0. Hence,
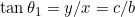
.
The
width of the image is then
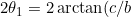)
. Constants vanish when we take the derivative and do not affect directionality of the stereo image.
I should track the maximum value of
r. Work out constraints later. Mid-Side
 \,=\, \sqrt{x^2 + y^2} \,=\, x\sqrt{1+c^2/b^2})
Plugging these values into (2)',
= 1- b+\sqrt{b^2 + c^2}, \;\;\; \tan\theta = c/b)
FIG3: Reference Signal
FIG3 Drag the red dot to change the angle of the source relative to the microphones.
Given two identical sources of equal magnitude, the same distance from the microphone, no two angles around the circle produce the same output. Disturbances reach the microphones from all directions, continuous in time, and the result is a
stereo image.
I will begin with the assumption that the imaging resolution is infinite. In other words,
if the membranes vibrate, then they will do so according to the laws of mechanics. The sensitivity of the membranes (and the bit depth of a resulting digital recording) determine the sensitivity to differences in phase angle.
Notes: Sound is a field. A sonic image is a relative map. It does not imply a knowledge of the absolute position of objects. A walk down the street with eyes closed should be enough to understand the division.
There is only so much time to spend on the implications of physics on the panner. The pan pot has no meaningful relationship to spatial imaging. Likewise, the surround speaker solution. It is expensive and reduces the imaging resolution to a handful of points in space. The sources of two sounds which arrive at different points at the same time are equidistant from both points. Changing the gain of the image at
playback, at the speaker has no relationship to position of a source in space. If it arrives at both ears at the same time, it is in front of us. Interpolation between speakers has the same relationship to 3-dimensional space as panning a static image across the screen. The illusion is vague and lacks flexibility. It is not a transformation which implies a change in relationship between the viewer and the image. If we layer and pan many images this way, adjusting the gain so each is "brightest" at its center, we have a collage.
Constructing a new space from scratch, and transforming it in time is a completely different question.
We distinguish the problems with our own approach. There is the "dead spot" at the center between the speakers. And now we have another speaker there. This is all nonsense. We all
also understand that a properly recorded stereo image creates an invisible column directly in front of us in space. An image too dense in the center can be widened, and new sounds placed in this invisbile column. The width of a stereo image is arbitrarily hight and can be adjusted with a single scalar.
If we choose to adjust the gain of mono files instead, certain observable properties result, which are independent of the number, or arrangement of speakers. Of particular note is the loss of an image between two speakers.
But imaging was the thing to be done. Interpolation is the most impoverished possible image given the technology at our disposal.
It remains to identify procedures we can carry out in the recording and mixing process which will allow us to leverage such images as orientable objects. Exactly as the visual artist.
Next up: Two sources at variable angles and distances.