{Under heavy editing. Incomplete}
Fig. 1
In Figure 1, source S moves along an arbitrary, directed path f(t). Microphones L and R and implied listener O' may be placed however we wish.
PROPOSITION:
To construct an image-preserving mapping from S to O'.
INITIAL ASSUMPTIONS
Arrange the listener and microphones in an equilateral triangle ΔLO'R:
All distances are in meters.
Let vL[n] and vR[n] be the voltage recordings at L and R, respectively:
Alternately,
Assume the recordings are normalized:
Let
ρ (rho) = sample rate of both recordings, in samples/second.
ψ (psi) = the constant speed of sound in meters/second
t = time in seconds
S is a physical object represented by a closed mesh.
Let
be the (magnitudes of) unknown disturbances propagating from S. Given initial time and orientation (t0, θ0, φ0) the amplitude in an arbitrary direction in the future is determined by the time t, and two angles θ, φ.
Specifically, assume μ is the result of a distinct motion in space, constrained to a small neighborhood of a central point m:(m1, m2, m3) within the bounding box of S. Further, assume μ(t, θ, φ) and point m imply one another. We have the inseparable tuple
I make no such assumption about σ(t, θ, φ). This distinction is essential.
Let
be a container for the image of S. X is a spatial picture: a 3-D "speaker" aligned with S, broadcasting into the game world.
The closure of the disturbance is the region enclosed by the maximum progression of the initial wavefront away from the source. In empty space, this is a sphere of radius tψ.
Ia. Point source (wave), Delay Only
If disturbances propagate in the air ideally (as a wave), μ reaches an arbitrary point x after a delay of T seconds. Considering only delay, the signal at x is identical to μ at some previous time t−T:
%20=%20\mu(t-T) "\small x(t) = \mu(t-T)")
where T is given by the distance from x to m:
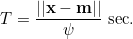
If S is a point source, X(t, μ, θ) is identical in all directions (we can ignore θ and φ),
 = X(t) "\small X(t,\theta ,\phi) = X(t)")
and there is a single generating function (σ is everywhere zero):
\;\;\;\;\;\;\; X(t) \,=\, \mu(t) \,=\, \int_{t_0}^t \! \textup{d}[\mu(t)]\textup{d}t \;=\; \int_{-\infty}^{\infty} \!\mu(\tau)\delta(t-\tau)\textup{d}\tau "\small (1)\;\;\;\;\;\;\; X(t) \,=\, \mu(t) \,=\, \int_{t_0}^t \! \textup{d}[\mu(t)]\textup{d}t \;=\; \int_{-\infty}^{\infty} \!\mu(\tau)\delta(t-\tau)\textup{d}\tau")
Now, consider the microphones at L and R.
If N is the number of samples corresponding to delay T over distance ||x − m||,
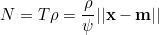
the recordings vL and vR can be given as delayed copies of μ:
 \;\;\;\;\;\;\;v_L =\mu[n-N_L], \;\;\; v_R = \mu[n-N_R] "(2) \;\;\;\;\;\;\;v_L =\mu[n-N_L], \;\;\; v_R = \mu[n-N_R]")
where
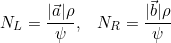
The delay ND between L and R is given by
\frac{\rho}{\psi})
ND is positive if ||b|| > ||a|| (...if the object is closer to the Right Microphone).
where T is given by the distance from x to m:
If S is a point source, X(t, μ, θ) is identical in all directions (we can ignore θ and φ),
and there is a single generating function (σ is everywhere zero):
Now, consider the microphones at L and R.
If N is the number of samples corresponding to delay T over distance ||x − m||,
the recordings vL and vR can be given as delayed copies of μ:
where
The delay ND between L and R is given by
ND is positive if ||b|| > ||a|| (...if the object is closer to the Right Microphone).
Ib. Attenuation by distance
The attenuation is a function of the distance the signal has traveled. Time (delay) and distance vary proportionately, and the variables can be exchanged accordingly. These transformations should be flexible. Use a placeholder, A(T):
 \;\;\;\;\;\;\;v_L =A(T_L)\mu[n-N_L], \;\;\; v_R = A(T_R)\mu[n-N_R] "(2b) \;\;\;\;\;\;\;v_L =A(T_L)\mu[n-N_L], \;\;\; v_R = A(T_R)\mu[n-N_R]")
X(t) is unchanged.
The signal is attenuated over the total distance traveled, and not the straight-line distance from source to microphone. In empty space, these two distances are the same. They will differ for reflections, transmission through other materials, moving objects, changes in the medium such as wind, etc.
Notes:
Ic. Attenuation by angleX(t) is unchanged.
The signal is attenuated over the total distance traveled, and not the straight-line distance from source to microphone. In empty space, these two distances are the same. They will differ for reflections, transmission through other materials, moving objects, changes in the medium such as wind, etc.
Notes:
As the signal travels outward, the wavefront lies on the surface of a sphere of increasing radius.
Surface area of a sphere: 4πr2
The ratio of surface area of two circles with radius r1, r2 is r12 / r22
An identical quantity distributed evenly over the two surfaces are in the proportion r22 / r12 units/m2.
Let the reference distance be a sphere of radius 1. Then at distance r,
(SA of r)/(SA of reference) = 1 / r2
The real amplitude C of harmonic motion described by a pair of complex roots is the square root of the sum of the square of two complex-valued coefficients.
C = 1/(√(c12 + c22)
Relevant functions: Inverse-square: A(x) = f(k 1/x2), Gauss: A(x) = f(ke-x2)
I will work out functions when I have a testable model. The ears will decide. Choice+constraints breed efficiency. But as with light, the choices should be convincing approximations of real phenomena.
Surface area of a sphere: 4πr2
The ratio of surface area of two circles with radius r1, r2 is r12 / r22
An identical quantity distributed evenly over the two surfaces are in the proportion r22 / r12 units/m2.
Let the reference distance be a sphere of radius 1. Then at distance r,
(SA of r)/(SA of reference) = 1 / r2
The real amplitude C of harmonic motion described by a pair of complex roots is the square root of the sum of the square of two complex-valued coefficients.
C = 1/(√(c12 + c22)
Relevant functions: Inverse-square: A(x) = f(k 1/x2), Gauss: A(x) = f(ke-x2)
I will work out functions when I have a testable model. The ears will decide. Choice+constraints breed efficiency. But as with light, the choices should be convincing approximations of real phenomena.
Suppose the Source is not a uniform, vibrating sphere. (It is not a point source. There is no such thing anyway.) It is an oriented object. S has both a position in space and an orienting unit vector es: 
. I have restricted the problem to two-dimensional space. Generalization to 3D introduces independent complications.
Generating motion μ(t) propagates non-uniformly in space. We can write
 \;\;\;\;\;\;\; X(t,\theta) =\xi(\theta)\mu(t) "(1c) \;\;\;\;\;\;\; X(t,\theta) =\xi(\theta)\mu(t)")
where μ(t) is attenuated by an angular damping function r = ξ(θ).
Equivalently,
Suppose there is some phenomenon in the neighborhood of S, damping σ(t) in such a way that attenuation is a function of angle, or
The function ξ(θ) is the volume envelope of σ(t).
The significance of the second statement will become apparent as the model develops.
For convenience, I will choose eS as the direction of maximum amplitude of X(t, θ).
is independent of the choice of function.
I accuse the family of cardioids of being not only fundamental to microphone design, but of generalizing naturally to spherical harmonics. (The latter's a guess, but come on).
We have
'\;\;\;\;\;\;\; X(t,\theta) \,=\, X(t,\vec x,\vec e_s)\,=\, \xi(\vec x, \vec e_s)\mu(t) "\small (1c)'\;\;\;\;\;\;\; X(t,\theta) \,=\, X(t,\vec x,\vec e_s)\,=\, \xi(\vec x, \vec e_s)\mu(t)")
I have declared the orientation to be a variable: es = es(t). The signal arriving at arbitrary, point x is now
 = A(T) \; \xi(\vec x, \vec e_s(t\!-\!T))\; \mu(t\!-\!T) "x(t) = A(T) \; \xi(\vec x, \vec e_s(t\!-\!T))\; \mu(t\!-\!T)")
where the vector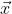
= (m−x).
The principal difficulty with this representation is that we must know the values of es going back to t−T. These difficulties will escalate as the model becomes more complex. Formally, I will rewrtie the equations as convolution sums and integrals to manage the indices. The fundamental analytic obstacle is to construct a transformation from listener to source. The purpose of a formal approach is to minimize such difficulties at the time of playback. Formal structures do not solve problems. I will not let abstraction lead me around by the nose.
An infinite number of such approaches are possible. I invent one.
We now have
\;\;\;\;\;\;\;\begin{align*} v_L[n,\vec e_s] &= A[N_L]\,\xi[\vec e_s(n\!-\!N_L)]\,\mu[n\!-\!N_L]\\ v_R[n,\vec e_s] &= A[N_R]\,\xi[\vec e_s(n\!-\!N_R)]\,\mu[n\!-\!N_R] \end{align*} "(2c)\;\;\;\;\;\;\;\begin{align*} v_L[n,\vec e_s] &= A[N_L]\,\xi[\vec e_s(n\!-\!N_L)]\,\mu[n\!-\!N_L]\\ v_R[n,\vec e_s] &= A[N_R]\,\xi[\vec e_s(n\!-\!N_R)]\,\mu[n\!-\!N_R] \end{align*}")
Note that we only need to rotate either L and R about S, or the Source via es. I choose to rotate es, and leave L and R fixed. The variable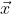
is replaced by normalized constants ea and eb, the unit vectors in directions 
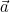and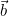 
respectively.
. I have restricted the problem to two-dimensional space. Generalization to 3D introduces independent complications.Generating motion μ(t) propagates non-uniformly in space. We can write
where μ(t) is attenuated by an angular damping function r = ξ(θ).
Equivalently,
Suppose there is some phenomenon in the neighborhood of S, damping σ(t) in such a way that attenuation is a function of angle, or
The function ξ(θ) is the volume envelope of σ(t).
The significance of the second statement will become apparent as the model develops.
For convenience, I will choose eS as the direction of maximum amplitude of X(t, θ).
- Example:
r = ξ(θ) is a cardioid with maximum value of 1, which occurs when θ = 0. The eS gives the orientation of the cardioid. Immediately, we have the magnitude of ξ(θ) in the direction of arbitrary vector x, for arbitrary orientation es
Of particular interest to me are the equations
...with the natural constraints -1 ≤ r ≤ 1, and/or where the area enclosed by the figure is constant as a, b, k are varied.
{I want visual tools for manipulating the image of linked stereo files}
{The mathematical elegance of the classic M/S stereo image warrant the approach.}
is independent of the choice of function.I accuse the family of cardioids of being not only fundamental to microphone design, but of generalizing naturally to spherical harmonics. (The latter's a guess, but come on).
We have
I have declared the orientation to be a variable: es = es(t). The signal arriving at arbitrary, point x is now
where the vector
The principal difficulty with this representation is that we must know the values of es going back to t−T. These difficulties will escalate as the model becomes more complex. Formally, I will rewrtie the equations as convolution sums and integrals to manage the indices. The fundamental analytic obstacle is to construct a transformation from listener to source. The purpose of a formal approach is to minimize such difficulties at the time of playback. Formal structures do not solve problems. I will not let abstraction lead me around by the nose.
An infinite number of such approaches are possible. I invent one.
We now have
Note that we only need to rotate either L and R about S, or the Source via es. I choose to rotate es, and leave L and R fixed. The variable
II. The Signal is Composite/Convolved
Suppose the second signal,
traverses m, and is subject to angular damping function
- Example:
, a pair of overlapping, circles.
Suppose the vibrating object is [can be written as] the convolution of two distinct functions. Declare an arbitrary point m. Adopt X(t) as above: μ(t) propagates identically in all directions from this point; attenuated by an envelope.
Now consider the second motion, σ(t). If the origin of σ is not be perfectly coincident with m, the disturbance σ(t) will traverse m in a uniform direction. In fact, every motion not coincident with m will traverse it a distinct direction.
This is exactly what we need to distinguish an image in the neighborhood of a point.
{Side signal mirrored across x-axis, but opposite "sign". σ(t) added to μ(t) on one side of sigma implies subtraction on the opposite side. σ(t), uncorrelated to μ(t) is a line gradient, not an image. M/S imaging immediately offers a means to ask a fundamental question:
Proposition: to widen the locus of sources about the point m, in such a way that a coherent image is constructed from two uncorrelated mono files.}
Case I: M and S are not correlated; i.e. the locus of points 1/2(1+cosθ) does not produce, when added (or convolved according to some function) to S, a field. The source is two uncorrelated mono files.
Case II: M and S are correlated. That is, it is also true that the signal at m relates all points not-coincident-with-m. Then the source is an image of arbitrary spatial resolution.
Proposition: To determine conditions necessary and/or sufficient to ensure M and S are an image
Proposition: To determine/define the cases under which it is desirable to
Proposition: To determine conditions necessary and/or sufficient to add (convolve) arbitrary signals in such a way that the relationship between the distinct objects is created in the image L R, heard at O'. (Example: Make sure all sound sources have directional noise components, and when mixing different sources correlate the noise.)
Proposition: To divide up the spatialization/audio pipeline into operational components:
1) The bulk of imagery is defined at the beginning and end of the pipeline by dense stereo image sources, and precomputed perspective transformations immediately prior to sample playback. Identical to lighting: the bulk of the information for transformation is a) precaptured, compact, variation-dense images and b) transforming those images only when they are seen by a view vector. Light is not actually ferried from place to place: images add to themselves based on the relative locations of light sources and viewer. Images are themselves sources of light (diffuse channel+global illumination = lit scene; image textures are of course captured from objects which are lit). We are generally concerned with ferrying large sources of white light from place to place.
2) Define sources of noise as a principal element of spatial construction, transformation, and coherence, by interaction with the environment and audio sources.
3) ddefine global (audio) illumination.
Background noise with no location. Follow the model of lighting. Precompute transformations with the environment. Mono nose file, looped, panned center provides no spatial information. Instead: A primary purpose of background noise should be to glue together the sounds into a coherent environment. Bad: Base global illumination lights objects by 1)adding low levels of broadband (noisy) light according to surrounding geometry/occlusion. 2) turning up and modulating pre-lit images defined on materials, 3) baking these values to tables/textures 4) adding these according to viewer position and angle.
4) Define methods for converting point sources (mono files) to spherical images. If the inside of the sphere is the operational space of our transformations, what can be done with mono files to achieve rich spatial properties at the surface of the sphere? Focus on widely applicable phenomena and types of motion: electricity, displacement, sympathetic vibration, irregularities of shape, buzzes, friction, strikes, transmission through materials, etc.
No comments:
Post a Comment