Snell's Law: Part The First

{Part  II −−>}

When light crosses from one medium to another of a different density, its speed and wavelength change.  Where it strikes the new surface at an angle, the transmitted wave is refracted, that is, the light changes direction.

Light which intersects a surface is incident.  The light which passes through the surface is transmitted.  The line perpendicular to a surface at a point p is normal to the surface at that point.   According to Snell's Law, we can assign to each medium a constant value η (eta), called its index of refraction (IOR), which satisfies the following relationship:
(1)                                                   η₁ sin θ₁ = η₂ sin θ₂ 
where η₁ and  η₂ are the indices of refreaction of the first and second media, respectively, θ₁ is the angle between the incident ray and the surface normal, and θ₂ is the angle between the transmitted ray and the normal.

Fig. 1

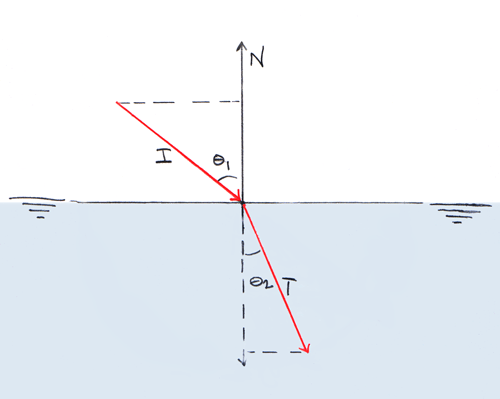
In Fig. 1, incident ray I strikes a new medium, and the transmitted ray T is refracted.  Each is shown as the hypotenuse of a triangle.  If both I  and T are drawn with a length of 1 (if they lie on a unit circle), then the opposite sides of the triangles will have lengths sin θ₁ and sin θ₂   (mouse over the image).  According to Snell's law, the relationship between these two lengths and their corresponding angles is completely determined by the constant ratio η₁/ η₂:

 

I will explore this equation in depth over several blog entries.

Assumptions

{  Edit: this section has been reworked.  I seek clarity in method and presentation.  If a question appeared here and vanished, I will visit it at a later point.  If you think I should retain, and strike, prior text  ( like so ) let me know.   Thanks to Peter Schaefer for assistance with assumption ii. }

i) The surface normal is vertical in the reference plane.
ii) The transmitted light will lie in the same plane as the incident ray and the surface normal.  In the diagram, there is a single transmitted ray.

The first assumption is made for simplicity.  For rigid geometric objects, relationships between angles are invariant under translation and rotation.  For example, if you print out Fig.1 and set it in front of you on the table, spinning the page around will not change the measure of any of the angles.  This problem is easier to solve for N = (0, 1) than for arbitrary N.

I assume (ii) as part of the definition of Snell's Law.  That is, it is a physical result. 
The difficulty is this.  As mentioned in the nVidia paper, equation (1) alone does not appear to restrict T to the same plane as  I  and N.  For, what is to prevent you from cheerily rotating T around the dotted line and forming a cone?  Nothing.  The interior angle remains θ₂ all the way 'round. Thus, by the Who's Going to Stop Me Theorem T need not lie in the given plane.  This may be done independently of a cheerful disposition.
However, I have given the incident ray and surface normal as vectors.  Together, I and N give the plane in which T will lie.  That is the point of the diagram.  I will state the restriction mathematically and account for it later, when I move the result to 3 dimensional space.

Onward.


For computation on graphics hadware, it is desirable to express Snell's Law in vector notation.   Thus,

Call the incident vector  I, the normal to surface N, and the transmission vector T. Assume I, T and N are normalized (each has a length of 1), and all lie in the same plane.  Then,
GIVEN: η₁, η₂, the indicies of refraction of the two media,
LET:
(2)  N = (0, 1)
      I = (–sinθ₁, cosθ₁)
     T = (sinθ₂, –cosθ₂)

The dot product of two normalized vectors gives the cosine of the angle between them.  Hence,
(3)   I•N = cosθ₁

I will also need the following trigonometric identity:

The Problem: Give T as a vector equation in η₁, η₂, N, and I.

This requires two steps , which may be done in any order.

I. Calculate T for any given η₁, η₂, N and I.

If I rewrite sinθ₁,  sinθ₂  and  cosθ₂  in terms of  cosθ₁ = I • N,  I can give each component of T as a vector equation.

sinθ₁ :  By (3) and (4), sinθ₁ becomes

sinθ₂ :  By Snell's Law (1),  sinθ₂ = (η₁ /η₂)sinθ₁   and by (4),

cosθ₂ :  Substituting this value of sinθ₂  into (4):


We can now give T = (sinθ₂, -cosθ₂):

This is correct, but in the vector T = (t₁, t₂), t₁ and t₂ have been solved separately.  I seek slightly more than this; I want to solve both simultaneously.  Hence,

II. Give T as the sum of two vectors.

Specifically, I want to write T as a linear combination of the two given vectors, N and I:

(9)        T      =     αI     +    βN ,         α, β constant:

       

This is another way of writing a pair of equations, with unknowns α and β:

(10)       sinθ₂ = –α sinθ₁

           –cosθ₂ =  α cosθ₁ +  β

α: The first equation gives α directly.   α =  –(sinθ₂/sinθ₁)   which, by (1), is

(11)       α = –η₁/η₂

β: Substituting this value of α into the second equation,

(12)       β = (η₁/ η₂)cosθ₁ − cosθ₂

Now the two steps can be merged.  Using the values for cosθ₁ and cosθ₂ in (3) and (7),

Substituting the values for α and β in (11) and (13) into T = αI + βN  gives  the desired relation:

                   

I have not derived a new formula, nor have I developed one of my own.  The above equation is an exact restatement of Snell's Law, in vector notation.

{Thanks to CodeCogs for their free LaTeX equation editor and image generation.}

{Part  II −−>}