I intend to finish Applied Vector Analysis in a month. 8 Chapters remain; most of the math I need is here.
- DifferentiationSpace curves
Surfaces
Tangent, curvature, torsion
- Divergence, Gradient, Curl
- Integration
Line, surface and volume integrals
Gauss' (Divergence) Theorem
Green's Theorem
Volume-to-surface; surface-to-line transformations
Irrotational Fields - Orthogonal Curvilinear Coordinates
CrippleSpecial coordinate systems
- Fluid Mechanics:
Equations of continuity, motion, and energy
Fluid States
Steady flow and streamlines
Vortex flow and circulation
- Electromagnetic Theory:
Electromagnetic field
Maxwell's equations
Potential
Energy and the Poynting vector
Static fields
Rad.
I'll take notes here.
I'll take notes here.
PARAMETRIC SURFACES: NORMAL VECTOR
The normal N to any surface represented by a vector function r(x,y) is given by
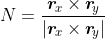
where
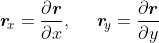
I. Explicit function of x, y
Let a surface S be given by the equations
 "x = x, \;\;\; y=y,\;\;\; z = z(x, y)")
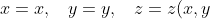where x, y, z are the coordinate axes. Then the position vector of any point on the surface is given by the vector function
= x \boldsymbol{\hat\imath} + y\boldsymbol{\hat \jmath} + z(x,y)\boldsymbol{\hat k} "r(x,y)= x \boldsymbol{\hat\imath} + y\boldsymbol{\hat \jmath} + z(x,y)\boldsymbol{\hat k}")
Compute the partial derivatives,
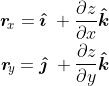
where
I. Explicit function of x, y
Let a surface S be given by the equations
where x, y, z are the coordinate axes. Then the position vector of any point on the surface is given by the vector function
Compute the partial derivatives,
Compute the cross product:
And the magnitude, for normalization:
\cdot (\boldsymbol {r}\!_x \times \boldsymbol {r}\!_y)} &\;\;=\;\; \sqrt{ \left( \frac{\partial z}{\partial x}\right)^2 + \left( \frac{\partial z}{\partial y}\right)^2 +1 } \end{align*} "\begin{align*} |\boldsymbol{r}\!_x \times \boldsymbol{r}\!_y| &\;\;=\;\; \sqrt{ (\boldsymbol {r}\!_x \times \boldsymbol {r}\!_y)\cdot (\boldsymbol {r}\!_x \times \boldsymbol {r}\!_y)} &\;\;=\;\; \sqrt{ \left( \frac{\partial z}{\partial x}\right)^2 + \left( \frac{\partial z}{\partial y}\right)^2 +1 } \end{align*}")
The normal vector to any point on the surface is then
^2 + \left( \dfrac{\partial z}{\partial y} \right)^2 +1}} "N \;=\; \frac{ -\dfrac{\partial z}{\partial x} \boldsymbol{\hat\imath}\; - \dfrac{\partial z}{\partial y} \boldsymbol{\hat\jmath}\; + \boldsymbol{\hat k}} {\sqrt{ \left (\dfrac{\partial z}{\partial x}\right)^2 + \left( \dfrac{\partial z}{\partial y} \right)^2 +1}}")
II. Implicit function of x, y.
I'm still not comfortable with partial derivatives of implicit functions. I lose the intuition quickly, and return to the definitions often.
Fix it, Ryan.
Okay. The following result makes me happy.
"
And the magnitude, for normalization:
The normal vector to any point on the surface is then
II. Implicit function of x, y.
I'm still not comfortable with partial derivatives of implicit functions. I lose the intuition quickly, and return to the definitions often.
Fix it, Ryan.
Okay. The following result makes me happy.
"
Problem 4-11 Find a unit normal vector n to a surface S that is represented by  = 0 "\phi (x, y ,z) = 0")
"
Go one step at a time. This is a surface. Any surface can be represented by a (series of) function(s) of two variables. So, the given function has two independent variables. Phi implicitly defines a function of two variables. By convention, I assume the independent variables are listed first, and are therefore x and y.
Phi defines z implicitly as a function of x and y.
Differentiate with respect to x:
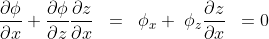
Solve for the partial of z with respect to x:
\;\;\;\;\;\frac{\partial z}{\partial x} \;=\;-\frac{\phi_x}{\phi_z} "(1)\;\;\;\;\;\frac{\partial z}{\partial x} \;=\;-\frac{\phi_x}{\phi_z}")
Differentiate with respect to y, and solve for the partial of z with respect to y:
\;\;\;\;\; \frac{\partial z}{\partial y} \;\;=- \frac{\phi_y}{\phi_z} \end{align*} "\begin{align*} &\frac {\partial \phi}{\partial y}\; + \frac{\partial \phi}{\partial z} \frac{\partial z}{\partial y} \;\;=\;\; \phi_y \, +\, \phi_z \frac{\partial z}{\partial y} \;\;=\;0 \\ &(2)\;\;\;\;\; \frac{\partial z}{\partial y} \;\;=- \frac{\phi_y}{\phi_z} \end{align*}")
Now, we have implicitly defined z as a function having the same form as the explicit equation in section I. Substitute the conspicuously Jacobian values (1) and (2) into the equations from I, and we now have the desired partial derivatives:
Again, the cross product:
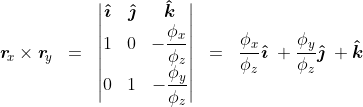
The relationship is clearer, and normalization simplified, if this is rewritten as:
 "\frac{1}{\phi_z}\left(\phi_x \boldsymbol{\hat\imath}\; + \phi_y \boldsymbol{\hat\jmath}\; + \phi_z\boldsymbol{\hat k}\right)")
Normalize!
^2 +(\phi_y)^2 + (\phi_z)^2}} "N = \frac{\boldsymbol {r}_x\times \boldsymbol{r}_y} {|\boldsymbol{r}\!_x \times \boldsymbol{r}\!_y|} &\;\;=\;\; \frac {\phi_x \boldsymbol{\hat\imath}\; + \phi_y \boldsymbol{\hat\jmath}\; + \phi_z\boldsymbol{\hat k}} {\sqrt{(\phi_x)^2 +(\phi_y)^2 + (\phi_z)^2}}")
Goodbye, extra z-partial.
^2 + \left(\dfrac{\partial \phi}{\partial y}\right)^2 + \left(\dfrac{\partial \phi}{\partial z}\right)^2 }} "= \frac{ \dfrac{\partial \phi}{\partial x}\boldsymbol{\hat\imath}\; + \dfrac{\partial \phi}{\partial y}\boldsymbol{\hat\jmath}\; + \dfrac{\partial \phi}{\partial z}\boldsymbol{\hat k}} { \sqrt{ \left(\dfrac{\partial \phi}{\partial x}\right)^2 + \left(\dfrac{\partial \phi}{\partial y}\right)^2 + \left(\dfrac{\partial \phi}{\partial z}\right)^2 }}")
Notes:
1. It is not clear to me why the implicit function is differentiated without reference to the unit vectors i, j and k. "Because it's implicit". Yeah. I get it. But rendering z = z(x,y) as a vector function is independent of the function's status as implicit or explicit. The answer is about measure, and I need to find it.
2. In the implicit function, it doesn't matter what x, y and z are. One of the three partial derivatives of φ is nonzero, or it does not meet the general definition of a surface. This nonzero partial corresponds to the dependent variable. I assume the partial derivative of φ with respect to z is nonzero. If it turns out to be x or y, the result can be computed in the same fashion.
The convention is for simplicity: list the dependent variables last. It saves the following step: suppose I intend to solve problem 4-11 and I require the dependent variable in the third position. Then I will solve the system
 = 0 "\phi (u, v ,w) = 0")
Phi defines z implicitly as a function of x and y.
Differentiate with respect to x:
Solve for the partial of z with respect to x:
Differentiate with respect to y, and solve for the partial of z with respect to y:
Now, we have implicitly defined z as a function having the same form as the explicit equation in section I. Substitute the conspicuously Jacobian values (1) and (2) into the equations from I, and we now have the desired partial derivatives:
Again, the cross product:
The relationship is clearer, and normalization simplified, if this is rewritten as:
Normalize!
Goodbye, extra z-partial.
Notes:
1. It is not clear to me why the implicit function is differentiated without reference to the unit vectors i, j and k. "Because it's implicit". Yeah. I get it. But rendering z = z(x,y) as a vector function is independent of the function's status as implicit or explicit. The answer is about measure, and I need to find it.
2. In the implicit function, it doesn't matter what x, y and z are. One of the three partial derivatives of φ is nonzero, or it does not meet the general definition of a surface. This nonzero partial corresponds to the dependent variable. I assume the partial derivative of φ with respect to z is nonzero. If it turns out to be x or y, the result can be computed in the same fashion.
The convention is for simplicity: list the dependent variables last. It saves the following step: suppose I intend to solve problem 4-11 and I require the dependent variable in the third position. Then I will solve the system
instead, where w is the dependent variable. Map the variables x, y, z in problem 4-11 to u, v, w accordingly as the surface function is known. I do not have to change a letter of the solution.
No comments:
Post a Comment