II. THE HOMOGENEOUS CASE, CONSTANT COEFFICIENTS
If Q(x) = 0, the equation is homogeneous.
(19.31)y^{(n)} \!+ f_{n-1}(x)y^{(n-1)}+ \cdots + f_1(x)y' + f_0(x)y = 0 \end{align*} "\small \begin{align*} f_n(x)y^{(n)} \!+ f_{n-1}(x)y^{(n-1)}+ \cdots + f_1(x)y' + f_0(x)y = 0 \end{align*}")
■ If the fk(x) are arbitrary functions of x, solutions of (19.31) are rarely expressible in terms of elementary functions. When they are, it is generally extremely difficult to find them. If the fk are constants, the general solution of (19.31) can always be found.
The homogeneous linear differential equation of order n with constant coefficients is thus
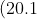\;\;\;\;\;\;\; a_n y^{(n)} + \cdots + a_1 y' + a_0 y = 0 "(20.1)\;\;\;\;\;\;\; a_n y^{(n)} + \cdots + a_1 y' + a_0 y = 0")
Now, the derivative of ex is ex. Also, ex is never ever ever ever zero, so we can divide it out of any equation, for all x. Using the Hey Wait a Minute... Postulate**, if we let
, then
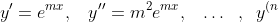}=m^{n}e^{mx} "y' = e^{mx}, \;\;\; y'' = m^2 e^{mx},\;\;\; \ldots \;\;,\;\; y^{(n)}=m^{n}e^{mx}")
Plugging this trial solution into (20.1) we have
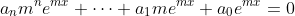
Divide through by emx,
 \;\;\;\;\;\;\; a_n m^n + \cdots + a_1 m + a_0 = 0 "(20.14) \;\;\;\;\;\;\; a_n m^n + \cdots + a_1 m + a_0 = 0")
.
Hey, aren't those all constants? Any value of m which satisfies this equation makes y a solution of (20.1). Our machinations are full of win.
■ Definition: Equation (20.14) is the characteristic equation of (20.1).
Sooooooo..... this is a regular-ass algebraic polynomial in m. It has at least one and not more than n distinct roots. We have n solutions of the form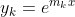
, with at least one, and not more than n, distinct values of n:
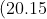 \;\;\;\;\; y_1 = e^{m_1 x}, \;\;\; y_2 = e^{m_2 x}, \;\;\; \ldots, \;\;\; y_n = e^{m_n x} "(20.15) \;\;\;\;\; y_1 = e^{m_1 x}, \;\;\; y_2 = e^{m_2 x}, \;\;\; \ldots, \;\;\; y_n = e^{m_n x}")
where the mk need not all be distinct.
We are confronted with three cases:
1. All of the roots are real, and distinct
2. All roots real, some multiple
3. All roots imaginary
All other cases are linear combinations of these three. The cases can be treated separately, and added together to form a composite solution yc. (The proofs are in Part I).
CASE 1: Roots of the Characteristic Equation Real
If all n roots, m1, m2, . . . , mn are distinct, (and extending the above proof), the n solutions y1, y2, . . . , yn are linearly independent. The general solution of (20.1) is thenIf Q(x) = 0, the equation is homogeneous.
(19.31)
■ If the fk(x) are arbitrary functions of x, solutions of (19.31) are rarely expressible in terms of elementary functions. When they are, it is generally extremely difficult to find them. If the fk are constants, the general solution of (19.31) can always be found.
The homogeneous linear differential equation of order n with constant coefficients is thus
Now, the derivative of ex is ex. Also, ex is never ever ever ever zero, so we can divide it out of any equation, for all x. Using the Hey Wait a Minute... Postulate**, if we let
Plugging this trial solution into (20.1) we have
Divide through by emx,
Hey, aren't those all constants? Any value of m which satisfies this equation makes y a solution of (20.1). Our machinations are full of win.
■ Definition: Equation (20.14) is the characteristic equation of (20.1).
Sooooooo..... this is a regular-ass algebraic polynomial in m. It has at least one and not more than n distinct roots. We have n solutions of the form
where the mk need not all be distinct.
We are confronted with three cases:
1. All of the roots are real, and distinct
2. All roots real, some multiple
3. All roots imaginary
All other cases are linear combinations of these three. The cases can be treated separately, and added together to form a composite solution yc. (The proofs are in Part I).
CASE 1: Roots of the Characteristic Equation Real
In this case, the procedure is straightforward. Solve for the roots m, and construct the solution. "Solve for the roots m" can be arbitrarily difficult, but it is at least a separate problem. Rad.
CASE 2: Roots of the Characteristic Equation Real, Some Multiple
{Coming back to this, I have an elementary example of Case I to work out. Simple but for the approach taken}
CASE 3: Roots of the Characteristic Equation Imaginary
{To Do.}
__________________________
**Squint one eye, make a serious face, and put your hands on your hips.At some point you may need to lean back and cross both arms over your chest.
No comments:
Post a Comment